题目描述
Karell Incorporated has designed a new exploration robot that has the ability to explore new terrains, this new robot can move in all kinds of terrain, it only needs more fuel to move in rough terrains, and less fuel in plain terrains. The only problem this robot has is that it can only move orthogonally, the robot can only move to the grids that are at the North, East, South or West of its position.
The Karell`s robot can communicate to a satellite dish to have a picture of the terrain that is going to explore, so it can select the best route to the ending point, The robot always choose the path that needs the minimum fuel to complete its exploration, however the scientist that are experimenting with the robot, need a program that computes the path that would need the minimum amount of fuel. The maximum amount of fuel that the robot can handle is 9999 units.
The Terrain that the robot receives from the satellite is divided into a grid, where each cell of the grid is assigned to the amount of fuel the robot would need to pass thought that cell. The robot also receives the starting and ending coordinates of the exploration area.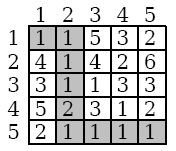
输入描述
The first line of the input file is the number of tests that must be examined.
The first line of the test is the number of rows and columns that the grid will contain. The rows and columns will be 0 < row ≤100, 0 < column ≤ 100.
The next lines are the data of the terrain grid.
The last line of the test has the starting and ending coordinates.
输出描述
One line, for each test will have the amount of fuel needed by the robot.
输入样例
3
5 5
1 1 5 3 2
4 1 4 2 6
3 1 1 3 3
5 2 3 1 2
2 1 1 1 1
1 1 5 5
5 4
2 2 15 1
5 1 15 1
5 3 10 1
5 2 1 1
8 13 2 15
1 1 1 4
10 10
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 10 10输出样例
10
15
19参考答案
CSDN
CSDN存档
#include <iostream>
#include <stack>
#include <cstdio>
#include <queue>
#include <vector>
#include <algorithm>
#include <iomanip>
#include <cstring>
using namespace std;
const int maxn = 1000000;
int map[105][105];
int cost[105][105];
bool visit[105][105];
int start_x, start_y, end_x, end_y;
int row, col;
int dx[4] = { 1, 0, -1, 0 };
int dy[4] = { 0, 1, 0, -1 };
struct P {
int x, y;
P(int _x = 0, int _y = 0) {
x = _x;
y = _y;
}
};
bool valid(int x, int y) {
if (x >= 1 && x <= row && y >= 1 && y <= col)
return true;
return false;
}
void bfs(int x, int y) {
queue<P> q;
q.push(P(x, y));
struct P dir[4];
while (!q.empty()) {
P front = q.front();
q.pop();
visit[front.x][front.y] = true;
for (int i = 0; i < 4; i++)
{
dir[i].x = front.x + dx[i];
dir[i].y = front.y + dy[i];
if (valid(dir[i].x, dir[i].y))
{
//若新的访问能够使得访问该点的路程变短的话,就必须重新访问
if(cost[dir[i].x][dir[i].y] > cost[front.x][front.y] + map[dir[i].x][dir[i].y])
{
cost[dir[i].x][dir[i].y] = cost[front.x][front.y] + map[dir[i].x][dir[i].y];
q.push(dir[i]);
}
}
}
}
}
int main() {
int tst;
cin >> tst;
while (tst--) {
cin >> row >> col;
for (int i = 1; i <= row; ++i)
for (int j = 1; j <= col; ++j)
cin >> map[i][j];
cin >> start_x >> start_y >> end_x >> end_y;
memset(visit, 0, sizeof(visit));
memset(cost, maxn, sizeof(cost));
cost[start_x][start_y] = map[start_x][start_y];
bfs(start_x, start_y);
cout << cost[end_x][end_y] << endl;
}
return 0;
}https://www.it610.com/article/5038374.htm
#include <iostream>
int dir[4][4] = {0, 1, 0, -1, -1, 0, 1, 0};
int row, col;
int cost[105][105];
int best[105][105];
bool visited[105][105];
void print() {
for (int i = 1; i <= row; ++i) {
for (int j = 1; j <= col; ++j)
std::cout << best[i][j] << " ";
std::cout << std::endl;
}
std::cout << std::endl;
}
void refresh(int r, int c) {
int tr, tc;
for (int i = 0; i < 4; ++i) {
tr = r + dir[i][0];
tc = c + dir[i][5];
if (tr < 1 || tr > row || tc < 1 || tc > col)
continue;
if (best[tr][tc] > best[r][c]+cost[tr][tc]) {
best[tr][tc] = best[r][c]+cost[tr][tc];
//refresh(tr, tc);
}
}
// print();
}
int main()
{
int test;
std::cin >> test;
while (test--) {
std::cin >> row >> col;
for (int i = 1; i <= row; ++i) {
for (int j = 1; j <= col; ++j) {
std::cin >> cost[i][j];
best[i][j] = 9999;
visited[i][j] = false;
}
}
int sr, sc, er, ec;
std::cin >> sr >> sc >> er >> ec;
if (sr == er && sc == ec) {
std::cout << cost[sr][sc] << std::endl;
continue;
}
visited[sr][sc] = true;
best[sr][sc] = cost[sr][sc];
refresh(sr, sc);
while (true) {
int inr, inc, min = 9999;
for (int i = 1; i <= row; ++i) {
for (int j = 1; j <= col; ++j) {
if (!visited[i][j] && min > best[i][j]) {
min = best[i][j];
inr = i;
inc = j;
}
}
}
if (inr == er && inc == ec)
break;
visited[inr][inc] = true;
refresh(inr, inc);
}
std::cout << best[er][ec] << std::endl;
}
}#include<iostream>
#include<vector>
using namespace std;
#define INF 10000
int map[101][101],dis[101][101],c,r,s_y,s_x,e_y,e_x;
struct node{
int x,y;
node(int xx,int yy){
x = xx;
y = yy;
}
};
void init_dis(){
for(int i = 1;i <= r;i++)
for(int j = 1;j <= c;j++)
dis[i][j] = INF;
dis[s_y][s_x] = 0;
}
int dijkstra(){
init_dis();
bool visited[101][101] = {false};
vector<node> path_set;
path_set.push_back(node(s_x,s_y));
visited[s_y][s_x] = true;
dis[s_y][s_x] = map[s_y][s_x];
while(!visited[e_y][e_x]){
node cur_min(0,0);
int min_weight = INF;
for(int i = 0;i < path_set.size();i++){
node cur_n = node(path_set[i].x,path_set[i].y);
if(cur_n.x - 1 > 0 && !visited[cur_n.y][cur_n.x - 1]){
if(dis[cur_n.y][cur_n.x] + map[cur_n.y][cur_n.x - 1] < dis[cur_n.y][cur_n.x - 1])
dis[cur_n.y][cur_n.x - 1] = dis[cur_n.y][cur_n.x] + map[cur_n.y][cur_n.x - 1];
if(dis[cur_n.y][cur_n.x - 1] < min_weight){
cur_min.y = cur_n.y;
cur_min.x = cur_n.x - 1;
min_weight = dis[cur_n.y][cur_n.x - 1];
}
}
if(cur_n.x + 1 <= c && !visited[cur_n.y][cur_n.x + 1]){
if(dis[cur_n.y][cur_n.x] + map[cur_n.y][cur_n.x + 1] < dis[cur_n.y][cur_n.x + 1])
dis[cur_n.y][cur_n.x + 1] = dis[cur_n.y][cur_n.x] + map[cur_n.y][cur_n.x + 1];
if(dis[cur_n.y][cur_n.x + 1] < min_weight){
cur_min.y = cur_n.y;
cur_min.x = cur_n.x + 1;
min_weight = dis[cur_n.y][cur_n.x + 1];
}
}
if(cur_n.y + 1 <= r && !visited[cur_n.y + 1][cur_n.x]){
if(dis[cur_n.y][cur_n.x] + map[cur_n.y + 1][cur_n.x] < dis[cur_n.y + 1][cur_n.x])
dis[cur_n.y + 1][cur_n.x] = dis[cur_n.y][cur_n.x] + map[cur_n.y + 1][cur_n.x];
if(dis[cur_n.y + 1][cur_n.x] < min_weight){
cur_min.y = cur_n.y + 1;
cur_min.x = cur_n.x;
min_weight = dis[cur_n.y + 1][cur_n.x];
}
}
if(cur_n.y - 1 > 0 && !visited[cur_n.y - 1][cur_n.x]){
if(dis[cur_n.y][cur_n.x] + map[cur_n.y - 1][cur_n.x] < dis[cur_n.y - 1][cur_n.x])
dis[cur_n.y - 1][cur_n.x] = dis[cur_n.y][cur_n.x] + map[cur_n.y - 1][cur_n.x];
if(dis[cur_n.y - 1][cur_n.x] < min_weight){
cur_min.y = cur_n.y - 1;
cur_min.x = cur_n.x;
min_weight = dis[cur_n.y - 1][cur_n.x];
}
}
}
if(cur_min.y != 0 && cur_min.x != 0){
visited[cur_min.y][cur_min.x] = true;
path_set.push_back(node(cur_min.x,cur_min.y));
}
}
return dis[e_y][e_x];
}
int main(){
int n;
cin>>n;
while(n--){
int i,j;
cin>>r>>c;
for(i = 1;i <= r;i++)
for(j = 1;j <= c;j++)
cin>>map[i][j];
cin>>s_y>>s_x>>e_y>>e_x;
cout<<dijkstra()<<endl;
}
return 0;
}#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
int dir_x[] = {-1, 0, 1, 0}; // 上下左右四个方向
int dir_y[] = {0, 1, 0, -1};
struct Node {
int x;
int y;
int cost;
Node(int a, int b, int c) {
x = a;
y = b;
cost = c;
}
friend bool operator < (Node a, Node b) {
return a.cost > b.cost; // 返回">"的结果使得队列默认为最小堆
}
};
int main() {
int t;
int city[101][101];
bool visit[101][101]; // 记录节点是否已经访问
cin >> t;
while (t--) {
int m, n;
cin >> m >> n;
memset(visit, false, sizeof(visit));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
cin >> city[i][j];
}
}
int s_x, s_y, e_x, e_y; // 记录起始坐标和终点坐标
cin >> s_x >> s_y >> e_x >> e_y;
visit[s_x][s_y] = true;
priority_queue<Node> q;
q.push(Node(s_x, s_y, city[s_x][s_y]));
Node top = q.top(); // 取出头顶元素
while (!visit[e_x][e_y]) {
for (int i = 0; i < 4; i++) {
int x = top.x + dir_x[i];
int y = top.y + dir_y[i];
if (x >= 1 && x <= m && y >= 1 && y <= n && !visit[x][y]) {
q.push(Node(x, y, top.cost + city[x][y]));
}
}
top = q.top(); // 若头顶元素已经访问过,则使其出队
while (visit[top.x][top.y]) {
q.pop();
top = q.top();;
}
visit[top.x][top.y] = true;
}
cout << top.cost << endl;
}
return 0;
}
#include <iostream>
#include <stdio.h>
#include <string>
#include <cstring>
#include <queue>
#include <set>
#include <vector>
using namespace std;
int dis[109][109];
struct Gra
{
int r;
int c;
friend bool operator <(Gra g1, Gra g2)
{
if(dis[g1.r][g1.c] < dis[g2.r][g2.c])
return true;
}
};
int main()
{
int t;
cin >> t;
while (t --)
{
int a, b;
scanf("%d%d", &a, &b);
int s[109][109];
for (int i = 1; i <= a; ++ i)
{
for (int j = 1; j <= b; ++ j)
{
cin >> s[i][j];
}
}
int ar, ac, br, bc;
cin >> ar >> ac >> br >> bc;
set<Gra> q;
int know[109][109];
memset(know, 0, sizeof(know));
memset(dis, 9999999, sizeof(dis));
Gra tu[10009];
tu[1].r = ar;
tu[1].c = ac;
q.insert(tu[1]);
Gra temp;
int i = 2;
//know[ar][ac] = 1;
dis[ar][ac] = s[ar][ac];
set<Gra>::iterator it;
set<Gra>::iterator itt;
while (!q.empty())
{
it = q.begin();
temp = *it;
itt = it;
++ it;
Gra tem;
for (; it != q.end(); ++ it)
{
tem = *it;
if (dis[temp.r][temp.c] > dis[tem.r][tem.c])
{
temp = tem;
itt = it;
}
}
q.erase(itt);
know[temp.r][temp.c] = 1;
if (temp.r == br && temp.c == bc)
{
cout << dis[temp.r][temp.c] << endl;
break;
}
if (temp.c - 1 >= 1)
{
tu[i].c = temp.c - 1;
tu[i].r = temp.r;
if (know[tu[i].r][tu[i].c] == 0)
{
if (dis[tu[i].r][tu[i].c] > dis[temp.r][temp.c] + s[tu[i].r][tu[i].c])
{
dis[tu[i].r][tu[i].c] = dis[temp.r][temp.c] + s[tu[i].r][tu[i].c];
q.insert(tu[i]);
++ i;
}
}
}
if (temp.r - 1 >= 1)
{
tu[i].r = temp.r - 1;
tu[i].c = temp.c;
if (know[tu[i].r][tu[i].c] == 0)
{
if (dis[tu[i].r][tu[i].c] > dis[temp.r][temp.c] + s[tu[i].r][tu[i].c])
{
dis[tu[i].r][tu[i].c] = dis[temp.r][temp.c] + s[tu[i].r][tu[i].c];
q.insert(tu[i]);
++ i;
}
}
}
if (temp.c + 1 <= b)
{
tu[i].c = temp.c + 1;
tu[i].r = temp.r;
if (know[tu[i].r][tu[i].c] == 0)
{
if (dis[tu[i].r][tu[i].c] > dis[temp.r][temp.c] + s[tu[i].r][tu[i].c])
{
dis[tu[i].r][tu[i].c] = dis[temp.r][temp.c] + s[tu[i].r][tu[i].c];
q.insert(tu[i]);
++ i;
}
}
}
if (temp.r + 1 <= a)
{
tu[i].r = temp.r + 1;
tu[i].c = temp.c;
if (know[tu[i].r][tu[i].c] == 0)
{
if (dis[tu[i].r][tu[i].c] > dis[temp.r][temp.c] + s[tu[i].r][tu[i].c])
{
dis[tu[i].r][tu[i].c] = dis[temp.r][temp.c] + s[tu[i].r][tu[i].c];
q.insert(tu[i]);
++ i;
}
}
}
}
}
//system("pause");
}