完全二叉树-最近公共祖先

题目描述
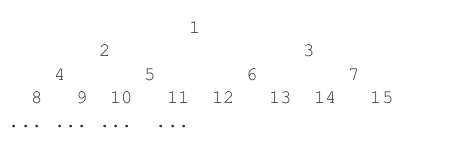
如下图，由正整数1，2，3，...组成一棵无限大的满二叉树。从某一个结点到根结点（编号是1的结点）都有一条唯一的路径，比如10到根节点的路径是(10,5,2,1)，由4到根节点的路径是(4,2,1)，从根结点1到根结点的路径上只包含一个结点1，因此路径是(1)。
对于两个结点X和Y,假设它们到根结点的路径分别是(X1,X2,...,1)和(Y1,Y2,...,1)(这里显然有X=X1,Y=Y1)，那么必然存在两个正整数i和j，使得从Xi和Yj开始，Xi=Yj,Xi+1=Yj+1，...，现在的问题就是，给定X和Y，要求Xi(也就是Yj)。

输入描述
输入的第一行是一个整数T，表示测试用例个数。以下T行，每行对应一个测试用例。
每个测试用例包括两个整数X和Y，这两个整数都不大于1000。

输出描述
对每个测试用例，单独一行输出一个整数Xi。

输入样例

2
10 4
7 13

输出样例

2
3

参考答案

#include <iostream>
using namespace std;

int common(int x, int y)
{
    if (x == y)//找到公共祖先
    {
        return x;
    }

    if (x > y)
    {
        return common(x / 2, y);//x的父亲节点 和y
    }

    return common(x, y / 2);//x和 y的父亲节点
}

int main()
{
    int group;
    cin >> group;
    for (int i = 0; i < group; ++i)
    {
        int m, n, result;
        cin >> m >> n;
        cout << common(m, n) << endl;
    }
}